The establishment of a photometric system for classification of White Dwarfs

The JeDi photometric system

Dmitrijus Semionovas
Jes Kristian Joergensen

Our task was to create and test a photometric system suitable for recognition and classification of white dwarfs. This system had also to be applicable for the classification of the main sequence stars.

As a starting point we assumed the interferometric variant of Vilnius photometric system, which was then ajusted and expanded to suit our purpose. To locate spectral bands, suitable for WD classification we used the ESO collection of spectrophotometric standards. Restricting ourselves to the wavelenghts suitable for the ground observations we chose to use 5 filters (W, P, X, Y, V) from the Vilnius photometric system (W and Y parameters were changed) and to employ 2 additional filters, E and Hb.

	W	P	X	E	Y	Hb	V
Lambda (A)	3500	3750	4060	4480	4600	4860	5470
Delta (A)	260	200	170	200	200	200	260

The reason of the choice of filters was as follows: W, P and X are used to measure the height of the Balmer jump. This is an effective measure of temperature for normal stars and it also can be used to recognize DA stars, which are the only white dwarfs with recognizable Balmer discontinuities. The P filter may be used as a pressure gradient gauge. Y filter presence was desirable due to its position of the knee of interstellar extinction law, so that it could be possible to employ the reddening correction procedures designed for Vilnius photometric system. The V filter is used for both temperature calibration and magnitude calibration for transformations between the systems. After some experiments Y filter position was shifted to the from 4660 A to 4600 A to avoid influence of H lines.

Two additional filters, E and Hb were chosen to monitor presence of He and H spectral lines, being positioned at HeI/HeII lines at 4480 A and H beta at 4859 A. All our filters were simple box functions which would not practically (and preferable in terms of the selectivity as the peak of the response curve carries more statistical weight that the wings) be the case.

We then created a small Fortran program, which read these spectra and calculated magnitudes in each filter normalized to the spectra of Vega. More precisely: For each filter the fluxes at the given wavelengths were summarized divided by the total number of measurements to make an average flux in the given filter and from this we calculated the magnitudes in the filters. With these given it's a simple task of subtraction to find the color indices, which could then be plotted in a color-color diagram.

As a primary color difference we chose temperature-dependent (Y-V). The following 5 color-color magnitude diagrams were used:

(Y-V) vs. (Y-Hb),
(Y-V) vs. (X-V) - (W-Hb),
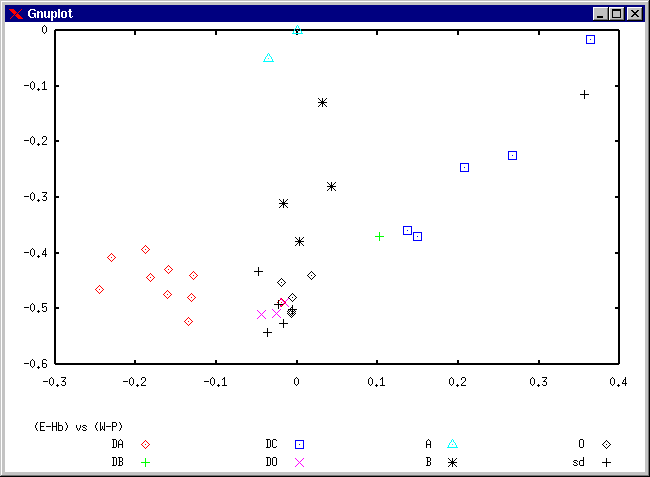
(Y-V) - (E-Hb) vs. (Y-V) - (W-P),
(W-P) - (Y-V) vs. (W-Hb) - (X-V),
(E-Hb) vs. (W-P)

The example of those color diagrams is shown below.

Fig. 1. Example of the color-color diagram.

Classification of the DA stars

If one examines the color diagrams like the one in appendix A one sees some features in the A dwarf population that are very interesting: The point corresponding to the white dwarf G138-31 falls quite of the sequence of the rest of the A dwarfs (also see the plot only including the white dwarf population in appendix B). If one considers the spectra of G138-31 compared to the rest of the A dwarfs one can also easily see that this should be the case (appendix C): The spectra peaks at around 4000 Å while the rest increases towards shorter wavelengths. We searched the internet for any litterature and also visited the White Dwarf Homepage to see if any studies of G138-31 had been done, but unfortunately it didn't seem to be the case. But in some way it proves that our photometric classification works since we're able to seperate out such white dwarfs.

The other point one might consider is whether these sequences corresponds to physical magnitudes. For A dwarfs this seem to be the case. If one considers the diagram in appendix B one notices the 3 dwarfs located in the lower part of the diagram. In the full diagram these are actually the ones that mixes with the main-sequence stars and O dwarfs. Again if one considers the spectra of these one notices that the spectra of these 3 dwarfs (appendix D) one notices that compared to the spectra of one of the "normal" A dwarfs it has almost no features in terms of hydrogen lines - so the sequence in A dwarfs in this diagram actually corresponds to a sequence in temperature.

Conclusion

Using those color-color diagrams we located regions specific to DC and DA WD stars and to B main sequence stars (and to the lesser precision those of O stars). Using the removal of "already classified" stars from the diagrams in principle was possible to differentiate to the certain precision between O and B main sequence stars, although this ineeds more investigation due to our limited sample of different stellar types representatives.

The most problematic was the classification of subdwarf stars, that were spread over most of the diagram phase space. This task could have been accoplished using one of standard methods of Vilnius photometric system (probably requiring inclusion of other filters from this system). It seems unlikely to distinguish between DB and DO white dwarfs using only wavelenghts accessible from the ground, as the far UV band carries a significant part of those stars spectral information.